Triángulos

El origen del triángulo se pierde en los albores de la historia.

Gracias a los restos arqueológicos hemos podido conocer que nuestros ancestros más primitivos ya conocían de su existencia y lo utilizaban en la construcción de herramientas y armas.

El antiguo Egipto, por otra parte, ya poseía avanzados conocimientos en geometría y utilizaba formas triangulares en muchos de los elementos que conformaban su arquitectura monumental.

Los babilonios, por ejemplo, eran capaces de calcular el área del triángulo (y otras figuras geométricas) para realizar las divisiones de los terrenos. 

Pero fueron los antiguos griegos quienes sistematizaron muchos de los conceptos geométricos que han llegado a nuestros días.

¿Qué es un triángulo?:

Un triángulo es un polígono de 3 lados.


Elementos del Triángulo:

-Vértices: son los puntos de intersección de las rectas cuyos segmentos determinan el triángulo.

–Lados: entre cada pareja de vértices se dibuja un segmento de recta que constituye un lado del triángulo.

–Ángulos: Entre cada lado con un vértice común se origina un ángulo, cuyo vértice coincide con el del triángulo.

Otros elementos:

Mediana: Es el segmento que une un vértice y el punto medio del lado opuesto al vértice.

Baricentro: Las tres medianas de un triángulo se cortan en un punto llamado Baricentro.
El Baricentro está al doble de distancia del vértice que del punto medio del lado opuesto.


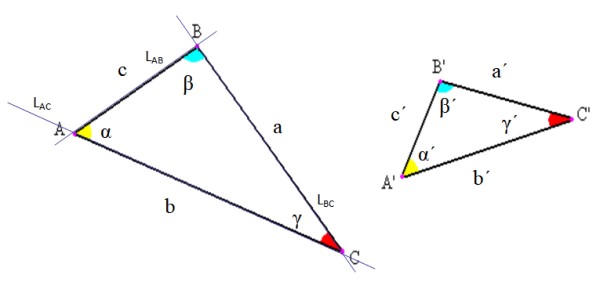
Notación del Triángulo:

Generalmente en la notación de triángulos se utilizan las siguientes convenciones: 

1. los vértices se indican con letras latinas mayúsculas 

2. los lados con letras latinas minúsculas 

3. los ángulos mediante letras griegas

4. Se nombra al triángulo según sus vértices. 

Por ejemplo el triángulo ABC, el triángulo A´B´C´...

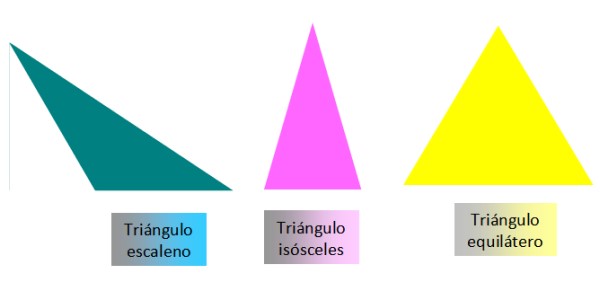
Tipos de Triángulos:

Según la medida de sus lados, los triángulos pueden ser: escalenos, isósceles o equiláteros:

-Escaleno: sus tres lados son diferentes.

-Isósceles: tiene dos lados iguales y uno diferente.

-Equilátero: los tres lados son iguales.

Propiedades de los Triángulos:

1. La suma de los ángulos internos de cualquier triángulo siempre es 180º.

2. Para cualquier triángulo, la suma de sus ángulos externos es igual a 360°.

3.  Un ángulo externo de un  triángulo es igual a la suma de los dos ángulos interiores no adyacentes a dicho ángulo.


Área de un Triángulo:

El área de un triángulo es su base por la altura dividido por 2

Trisección de un Ángulo

En la Antigua Grecia se consideraban Problemas Planos a todos aquellos cuya solución podía hallarse mediante el uso de rectas y circunferencias, es decir, utilizando únicamente la regla y el compás.

La regla y el compás, eran considerados los instrumentos de dibujo más precisos.

La circunferencia fue la primera línea curva plana que apareció en la geometría griega. 

Los griegos también aceptaron como Curvas Geométricas, aunque no fueran construibles con regla y compás, la elipse, la parábola y la hipérbola, porque las tres se  podían generar por intersecciones de un plano con un cono. 

Todas las demás curvas que no podían construirse con regla y compás quedaron fuera de la Geometría Pura y fueron llamadas Curvas Mecánicas, ya que se formaban por el movimiento de un punto bajo ciertas condiciones.

Para los griegos estas curvas carecían de la pureza y de la belleza matemática que sí tenían las curvas geométricas.

Algunos geómetras griegos se interesaron por las Curvas Mecánicas para tratar de resolver con ellas alguno de los tres problemas clásicos griegos que eran: la cuadratura del círculo, la duplicación del cubo  y la trisección del ángulo, los cuales se resistían a ser resueltos con la regla y el compás.

Una de las trisecciones que sí pueden lograrse con regla y compás es la de un ángulo recto.

Para realizar la división de un ángulo recto en 3 partes iguales seguiremos los siguientes pasos:

1. Se traza un ángulo recto con escuadra y cartabón.
2. Se coge un radio cualquiera y con centro en el vértice O se traza un arco que cortará los lados del ángulo en los puntos A y B
3. Manteniendo el mismo radio y haciendo centro en los puntos A y B, se trazan dos arcos que al cortarse con el anterior darán lugar a los puntos 1 y 2.
4. Uniendo el vértice O con los puntos resultantes 1 y 2 obendremos las 3 partes iguales del ángulo recto inicial.

 

 Video:

 

Ejercicio:

 

1. Dibuja un círculo de 5 cm. de radio.

2. Dibuja un diámetro (siempre pasa por el centro). 

3. Dibuja otro diámetro que haga 90º con éste.

4. Divide los 4 ángulos rectos resultantes en 3 partes iguales utilizando el anterior método (Trisección) de manera que el círculo quede dividido en 12 partes iguales.

5. Utiliza las áreas resultantes para hacer un círulo cromático de manera que los 3 colores primarios aparezcan a igual distancia ente sí y entre ellos se desarrollen los colores secundarios y terciarios.

Curiosidades:

Dibuja como los antiguos griegos : Ancient Greek Geometry